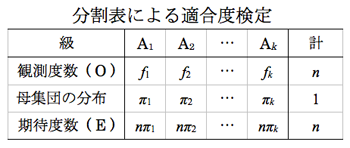
コンプリート! 期待度数 求め方 236406-期待度数 求め方 エクセル
40 計 65 35 100 × 35/100 × 35/100 24 検定の方針 期待度数 治った 治ら2×2分割表、l×m分割表 2×2分割表 X 2 適合検定ではひと続きの独立なデータとして分類した。 それに対し、2×2分割表は行・列がそれぞれ二方向ある分類である。 X 2 適合検定で観測度数と期待度数の偏りを計算してX 2 値を求めたのと同じように、2×2分割表の計算でも観測度数と期待度数の偏りを一番右の列と一番下の列の数値から、 4カテゴリで関連がなかった時の「期待度数」 を算出した表です。 期待度数の算出は以下の通り。 例えば薬剤群で治った人のカテゴリに関する期待度数。 これは、全40人のうち、人が薬剤群です。
2群間の差の検定 カイ二乗検定 T Nakaの阿房ブログ
期待度数 求め方 エクセル
期待度数 求め方 エクセル-この記事では、カイ二乗検定とT検定の自由度のでの求め方とその意味を、例題を使って解説します。 >>もう統計で悩むのは終わりにしませんか? ↑1万人以上の医療従事者が購読中 Contents 自由度とは?求め方や意味をわかりやすく;観測度数Oiと期待度数Eiの全体のずれが偶然起こったものであるなら、ここで求めたX 2 値はX 2 に従う。ただし自由度dfは理論度数によって異なり、下のようになる。 ・一様分布のとき、df=k1 ・二項orポアソン分布のとき、df=k2 ・正規分布のとき、df=k3
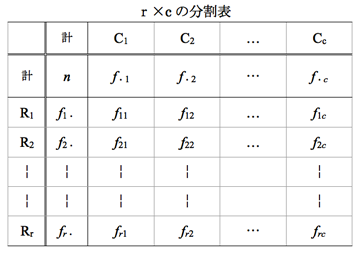



カイ二乗検定 日経リサーチ
期待値の求め方例題 実際に例題で期待値の公式を使ってみましょう。 例題 サイコロを \(1\) 個振ったときに出る目の期待値を計算せよ。 まずは「確率変数 \(X\)」「\(X\) がとる値」「\(X\) がその値をとる確率」をそれぞれ求めます。 慣れない間は確率分布表を作るとわかりやすいですT検定とカイ二乗検定の違い こんにちは、リーンシグマ、ブラックベルトのマイク根上です。 今日はこの動画リクエストからです。 「いつも度数分布表の中央付近で,仮変数 0 にすると大きい方も小さい方も ±2 のように小さな整数値になって,計算が楽になるからです.先頭を 0 から始めて(仮平均を他の値に設定しても,例えば325としても)も正しく求めることはできますが,階級値の仮変数として, 0,1,2,3,4 などとすると数字が
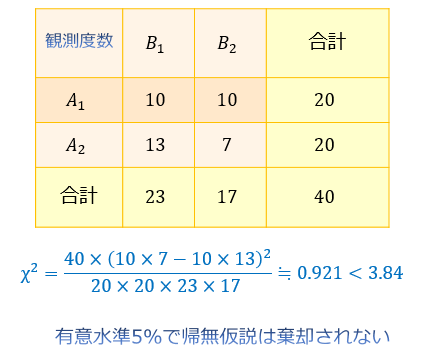
χ2検定の数式 (ChiSquare Distribution) 数式中のΣは、総和を示します。 期待値(期待度数)の求め方 ・\(p=23/40\) より、それぞれ \(×23/40=115\) 回ずつ成功して \(85\) 回ずつ失敗することが期待される(期待度数) 式に代入して計算すると、\(\chi^2≒0921\) と求まりました。 サイコロの目の出方に偏りがないかどうかを調べるために サイコロを1回振って出た目の数を調べた。 期待度数は、各目で(1/6) 観測度数は、1回の試行で得られた各目の回数 この場合は期待度数は一定で
期待値の定義・省略表記 期待値は、 確率変数 X の「取りうる値 x 1,x 2,,x n 」と「その値をとる確率 p 1,p 2,,p n 」の積の合計として求められる値です。 期待値は英語で Expected Value という事から、省略して EVと表記される こともあります。期待値は別名期待度数などとも呼ばれます。 期待値の計算式としては、ある事象が起こる確率をp1、p2・・・+pnとし、各々の事象における数値をx1、x2+・・・xnとしたとき期待値=p1x1 p2x2 ・・・・ pn xn と表現されます。実測値範囲と期待値範囲に含まれるデータの個数が異なる場合、エラー値 #N/A が返されます。 χ2 検定では、次の数式を使用して、まず χ2 統計量が計算されます。 ここで Aij = i 行 j 列内の実測値の度数 (実測値頻度) Eij = i 行 j 列内の期待値の度数 (期待値




X二乗検定の期待度数が求められません Logics Of Blue Com 統計学 教えて Goo



Q Tbn And9gcr5g5a N3oo Zlp2eeelne3fwyfirfizw Nw7oqmlzrgcse1oyi Usqp Cau
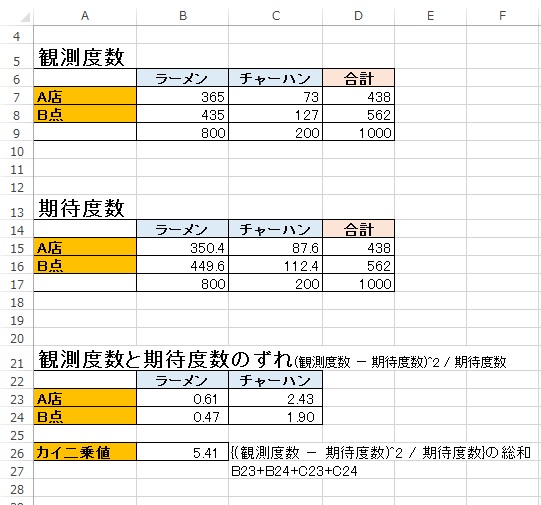
観測度数と期待度数を元にして、カイ2乗値を計算します。 カイ2乗値=(((観測度数-期待度数)の2乗)÷期待度数)の総和 =(全部で6個のマスについて計算します) = = = (小数点第3位を四捨五入) となります。 自由度を求める 自由度は、次のように求まります。 自由度=(行の数-1 クロック数の期待値 = 4 クロック × 30 % + 8 クロック × 60 % + 10 クロック × 10 % = 7 クロック 700 MHz のクロック信号が与えられているので、1 秒間に実行できる命令数を百万単位で示すと、以下のように 100 百万個になります。期待値 = 100⋅ 1 10 0⋅ 2 10 300⋅ 3 10 400⋅ 4 10 = 100 1 10 0 2 10 300 3 10 400 4 10 = = 10 40 90 160 = 300 = 300 期待値は300円りになります. また,次のように考えることもできる. カードの引き方が同様に確からしいとすると,10回カードを引くとすべてのカードを1回ずつ引くことになる.すると, 1のカードを引いて100円もらえるのが1回 2の



スポーツ健康科学部ブログ あいコアの星 立命館大学




カテゴリデータの関係性を検定 Excelでできるカイ二乗検定 2年でデータサイエンティストになった人が教える 初心者のためのイメージで分かるai データ分析
期待度数 「期待される値」でなく「期待される度数」と覚えると、混乱しないかも知れません。 " 期待度数 = (i行の計 x j列の計) / 総合計 " で定義される為、 つまり 治療A有効の期待数は35× (7/55)=445 治療B有効の期待数は× (7/55)=255 治療A無効の期待数は35× (48/55)=3055 治療B無効の期待数は× (48/55)=1745 となります。 これが期待数の求め方です。 2×2マスで比率を比較する場合、 1つでも期待数5未満がある場合 はカイ2乗検定は不適切となるようです。 今回の例ではFisherの正確検定を用いるのが正解となります。サイコロは、どの面も出る確率が\(\frac{1}{6}\)である点に注意して計算すれば、期待値はすぐ求められます。 連続確率変数の例:確率密度関数\(p(x) = \frac{1}{6}\)で確率変数が\((0 \leq X \leq 6)\)の範囲で値を取るときの期待値を考えます。




カイ二乗検定
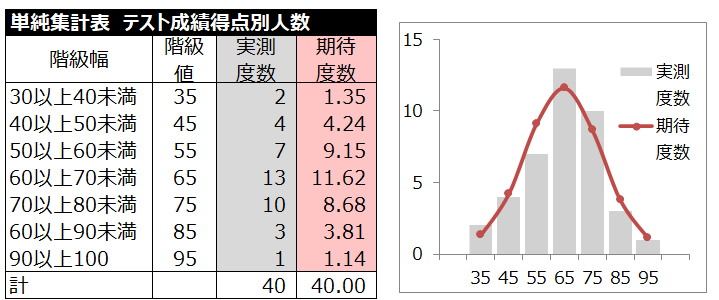



度数の検定 株式会社アイスタット 統計分析研究所
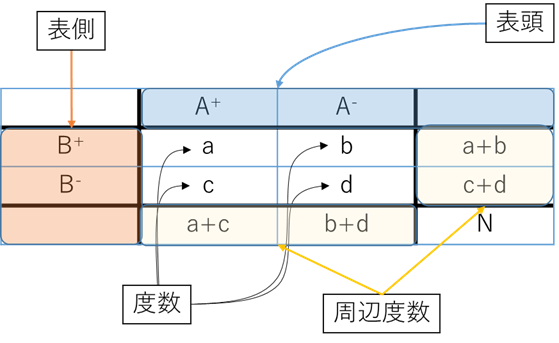
ちなみに、期待度数は で求められる。 カテゴリー 1 2 計 n₁₁ n₁₂ n₂₁ n₂₂ n₁ n₂ 計 n₁ n₂ N 1 2 カ テ ゴ リ ー カイ二乗検定を行うときの注意 条件間に対応のないケースのみ使用可能 ⇒対応がある場合、マクネマー検定、コクランのQ検定 など、他の検定を使う。 観測度数が少ない# Õ0ê0ü0½0Õ0È0k0ˆ0‹0Ç0ü0¿0㉠gû0Þ0¤0Ë0ó0°0,{66ÞV q} Š„vÆ00¹0È0㉠g(11)^ÿÆ00¹0È0k0J0Q0‹0 RrRhˆn0 R g^ÿこのクロス表から期待度数の推定値を計算すると、次のようになる。 期待度数の推定値 幸福度 あまり幸せでない けっこう幸せ とても幸せ 家族の収入 平均より上 3577 15 平均 7968 平均より下 5255 Excelでχ 2 検定(独立性の検定)を行う Excelで数




Ezrでfisherの正確検定を行う方法 深kokyu



カイ2乗分布 カイ2乗検定
測定値 度数 相対度数 度数分布表について詳しく知りたい方は こちら を参照してください. この表から,確率変数の平均 というのは以下のようにして求めることができます. ここで,上式ではN→∞で相対度数が確立となっていることに注意して3 カイ2乗検定 ←前へ もくじ 次へ→ 毎日お店に来ては、ポテトの長さを調べたりお客さんのポテトを数えていたあなた。観測度数と期待度数 期待度数:2変数間に関連がない(確率的に独立であ る)ときの度数の期待値 ≤ < ∞ − = 2 2 2 0 ( ) ( ) χ χ 期待度数 観測度数 期待度数 カイ二乗値 6 性別 と 血液型 のクロス表 52 29 35 13 129 493 310 371 117 1290 45 32 38 10 125 477 300 359 113 1250 97 61 73 23 254



Http Science Cc Kochi U Ac Jp Scientific Reports Vol02 Serfst1909 Pdf



Rで統計学を学ぶ 4
Pythonでカイ二乗検定を行う場合、 scipystats の chi2_contingency 関数を使います。 scipystatschi2_contingency|公式サイト (英語) chi2, p, dof, ef = scipy stats chi2_contingency ( df, correction =False) 結果は、 統計量、p値、自由度、期待度数の表の順に出力されます。 標準だと atusirさん 期待度数 (理論度数)の定義は、 E (i,j)=N (i,・)N (・,j)/N です。統計学の適合性検定の問題なのですが、この場合の期待度数はどのように求めればいいのでしょうか? 帰無仮説は、「好みはどれも同じ」である 全体40匹。 4つの果物に向かうので、 好みがなければ(期待度数は)40/4=10




カイ二乗検定のわかりやすいまとめ Avilen Ai Trend




統計検定2級 2018年6月の 問15 1 日経新聞を読んだ感想
期待度の確率より期待度数を求め、p4と同様に統計量Tを算出します。閾値は、自由度が2となりますので、p7の分布表を求めます。この場合も帰無仮説は 棄却 され、 独立性はないと判定 されます。 p9 Minitabの実行例です。p6と同様です。実測度数,期待度数,帰無仮説,有意水準などの用語を理解する。 定義式に基づいてχ 2 を計算して検定する。 Excel関数を使ってχ 2 検定を行なう。 Excel の関数 chiinv (a,n)・・・自由度n ,有意水準 aに対する χ 2 を与える chidist (χ 2,n)・・・自由度n に対する確率 P(>χ 2)を与える 2)を与える 例題周辺度数を固定したときに,帰無仮説のもとでの各セル期待度数は, 帰無仮説のもとでの期待度数 成 功 失 敗 試行 X (a b)(a c)/N (a b)(b d)/N 試行 Y (c d)(a c)/N (c d)(b d)/N となる.すると,ピアソンの χ 2 値は,成功確率が等しいという帰無仮説のもとで, 自由度 1 の χ 2 分布に従う



2群間の差の検定 カイ二乗検定 T Nakaの阿房ブログ
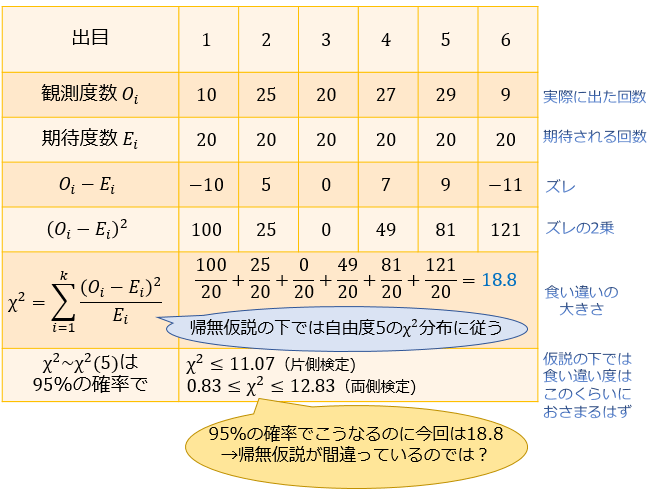



カイ二乗検定 適合度検定の計算法を例題から解説 確率の偏りに惑わされないための統計的検定とは アタリマエ
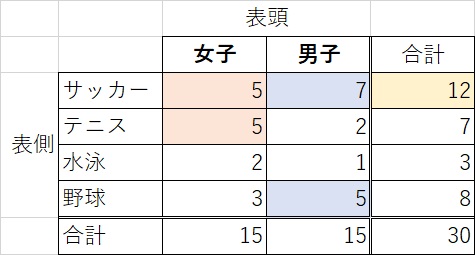
これらの観測度数と期待度数について,前の例1と同様にカイ2乗値を求める. χ 2 = =697 自由度2,有意水準5%のときχ 2= 599 599<697 だから有意差があり,育て方と製品の等級には関連があ 期待度数は「横計*縦計/全合計」です。 たとえば、期待度数の 男: 赤:135人は 360 (男合計)*225 (赤合計)/600=135 で計算された値です。例えば,期待値lambda=5のポワソン分布において,実際に4回となる確率は,dpois(4, lambda= 5) で求められ,0回から4回となる累積確率は ppois(4, lambda= 5) で求められる。累積確率は,0回,1回,2回,3回,4回となる確率の合計であるが,これらの確率は dpois(04, lambda= 5) とすればそれぞれ求められる
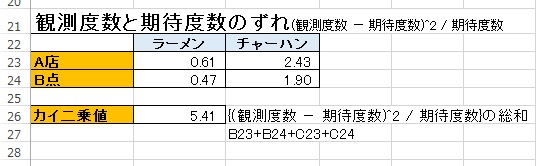



カイ X 二乗値とカイ二乗検定 優技録



Kh Coder 掲示板
期待度数の求め方 4 / 4 • 薬を飲まないで治らなかった人の期待度数 薬を飲まなかった人 40人 (100人中) 治らなかった人 35人 (100人中) ⇒ 40 × 35/100 = 16人 期待度数 治った 治らなかった 計 薬飲んだ 39 21 60 薬飲まなかった 26 ??期待 度数 求め 方 科研 費 英語 表記 損益 分岐 点 売上 高 求め 方 膿瘍 形成 性 虫垂炎 白黒 画像 カラー 化 緯度 経度 距離 計算 発達 障害 研究 所 関東 地方 花火 大会 戦後 70 年 ニッポン の 肖像 カイ二乗検定 適合度検定の計算法を例題から解説 確率の偏りに惑わされないための統計的検定




2 2の分割表の活用 実験データの具体的な解析方法
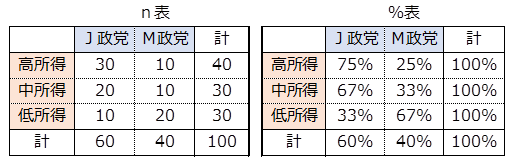



カイ2乗検定 クラメール連関係数 1 2 株式会社アイスタット 統計分析研究所
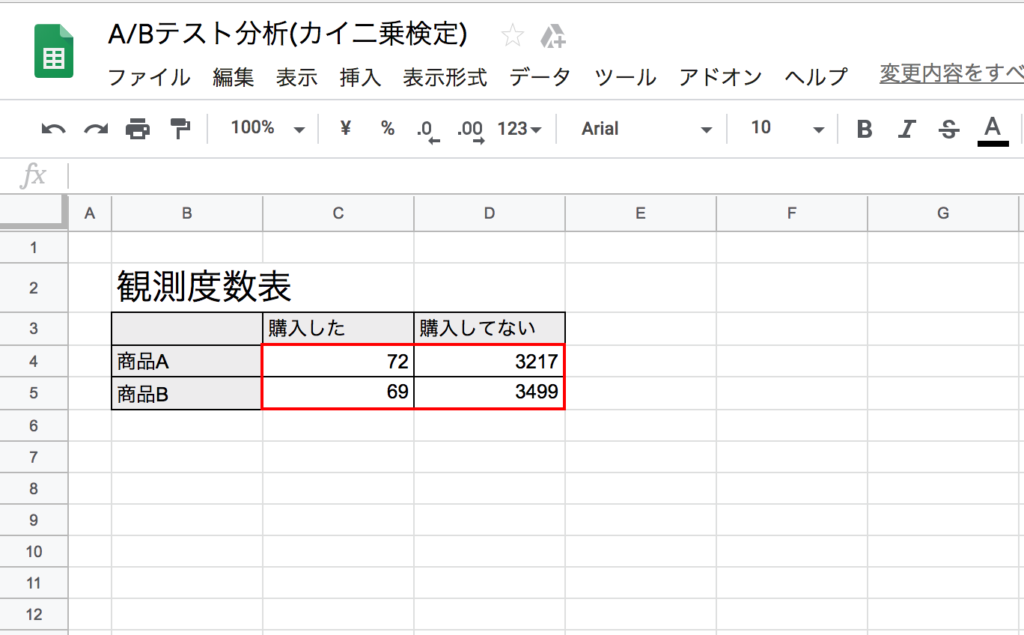



スプレッドシートでピアソンのカイ二乗検定 独立性の検定 を行う方法 たぬハック




分布の適合度検定を行う カイ二乗検定 Python Biotech ラボ ノート



2



統計講座



Http Cogpsy Educ Kyoto U Ac Jp Personal Kusumi Datasem11 Kumaki Pdf




カイ二乗検定とは 分かりやすく例で分割表の検定の計算式も簡単に いちばんやさしい 医療統計




応用情報処理 第8回 適合度 独立性の検定 練習問題2




X2検定2 1変量




適合度検定をカイ二乗検定で行う例題と手順 Avilen Ai Trend



ノンパラメトリックな検定 u検定とカイ二乗検定




X2検定1 2変量
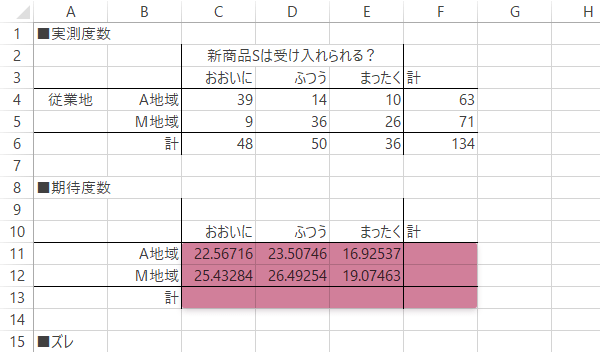



クラメールの連関係数の計算 With Excel



Http Www1 Tcue Ac Jp Home1 Ymiyatagbt Chisquare Test Pdf




黒木玄 Gen Kuroki 統計 誤解の事例を追加 T Co Vyvplucx2j カイ2乗検定 奥村晴彦 Last Modified 19 01 09 10 30 29 分割表のx 検定はサンプルの周辺度数 縦横の合計 が確率的に揺らぐ場合にも有効 むしろそういう場合の方が有効 なので 自由度




カイ二乗検定 日経リサーチ




エクセルexcelでx二乗検定を
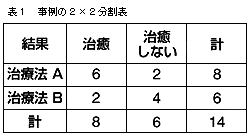



医学書院 週刊医学界新聞 連載 実践統計学入門 第2245号 1997年6月23日




統計ことはじめ クラメールの連関係数 Neo Log



クロス集計表で質的変数を検定しよう ピアソンのカイ二乗検定 シグマアイ 仕事で使える統計を




Brvnt4arzhmsym




カテゴリデータの関係性を検定 Excelでできるカイ二乗検定 2年でデータサイエンティストになった人が教える 初心者のためのイメージで分かるai データ分析



カイ二乗検定 Logics Of Blue



統計的テキスト解析 11 テキストにおける分割表の分析




Step24 看護研究 推測統計の手法 その2 ナース専科




X2分布




jmpによるデータ分析 グラフ作成15 眼科医と眼科専門mrのためのデータ分析あれこれ



Q Tbn And9gcqbb Ik0kux1ye7hezfl7naut4z Ru4fhdfdcpksvysuqcl 3y7 Usqp Cau




酢語録blog 統計学 カイ二乗検定でサクッとp値を求める



Http Univ Obihiro Ac Jp Kayano Epi Stat H27biostat4 Pdf




統計検定二級の問題です 期待度数の問題です わかる方お願いします Clear



第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計



Http Www Ner Takushoku U Ac Jp Masano Class Material Waseda Keiryo R13 Chi Correlation Html




その 現場のカン は本当に正しい 現場のカン の確からしさを検証するには Digital オペレーションを進化させる現場のwebマガジン 現場ドリブン




X2検定1 2変量




応用情報処理 第8回 適合度 独立性の検定 練習問題2




独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend



株 日科技研 カイ二乗検定とは 信頼性解析 製品案内




カイ2乗検定



独立性の検定をstataで実行する 医療統計とstataプログラミングの部屋




独立性のカイ二乗検定 例題を用いてわかりやすく解説 Avilen Ai Trend




カイ二乗検定 X2検定 について優しく図解 わかった気になる ふわっと理解 小学校の知識でわかる統計辞書



統計的テキスト解析 11 テキストにおける分割表の分析



気象の統計学 台風は火曜日が好き 片山由紀子 個人 Yahoo ニュース
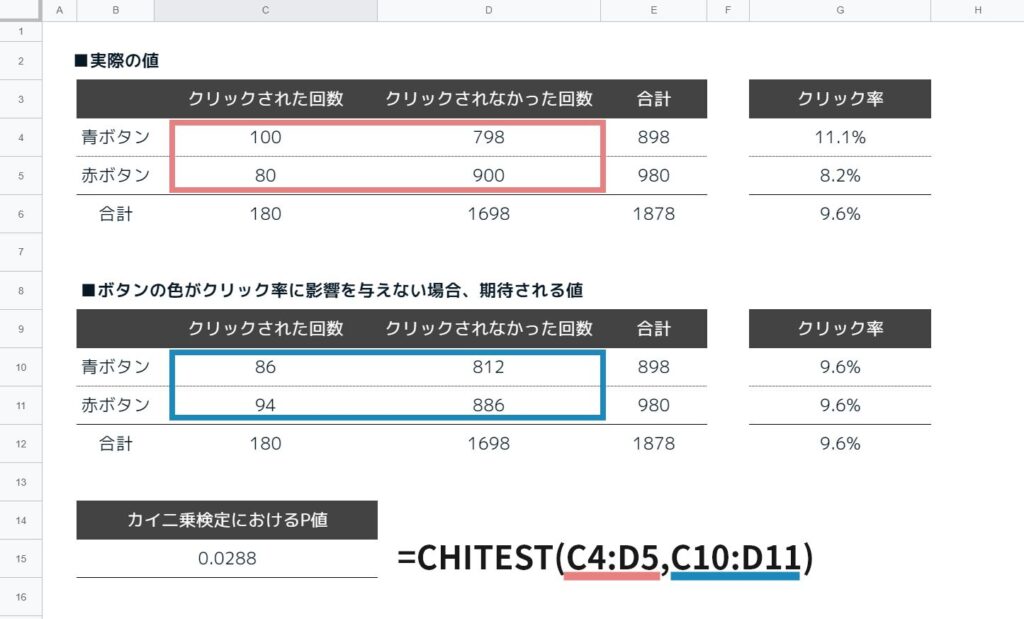



その分析結果は偶然ではありませんか カイ二乗検定 独立性の検定 で確かめる Chitest関数 Zizi Tips




Abテスト カイ二乗検定 で使われる ピアソンの カイ二乗値 と カイ二乗値 の違いを理解 検証する ピアソンのカイ二乗値の分母が期待度数である理由 Qiita
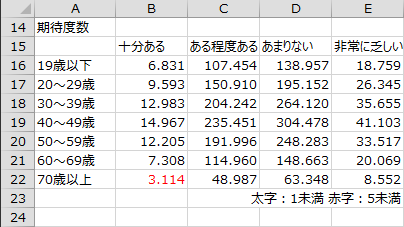



独立性の検定 エクセル統計による解析事例 ブログ 統計web
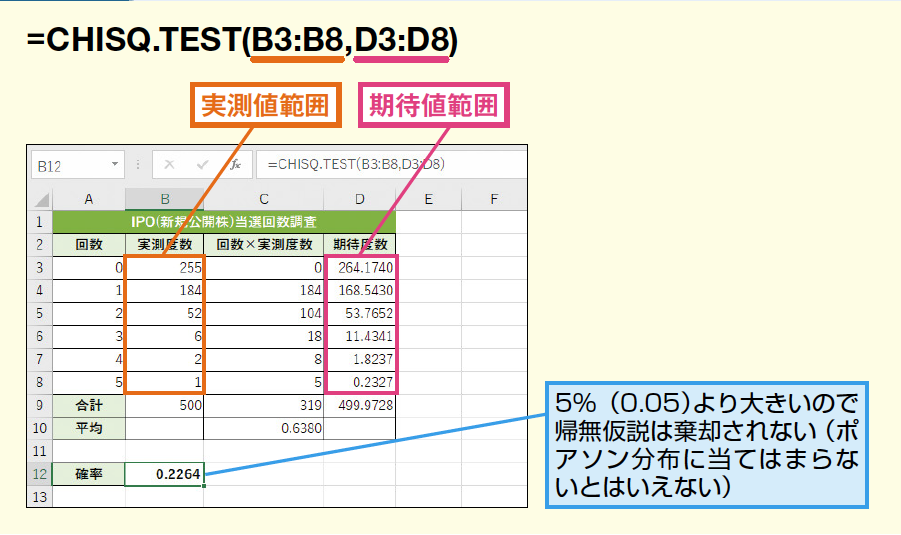



Chisq Test関数 Chitest関数でカイ二乗検定を行う Excel関数 できるネット



カイ二乗検定 日経リサーチ
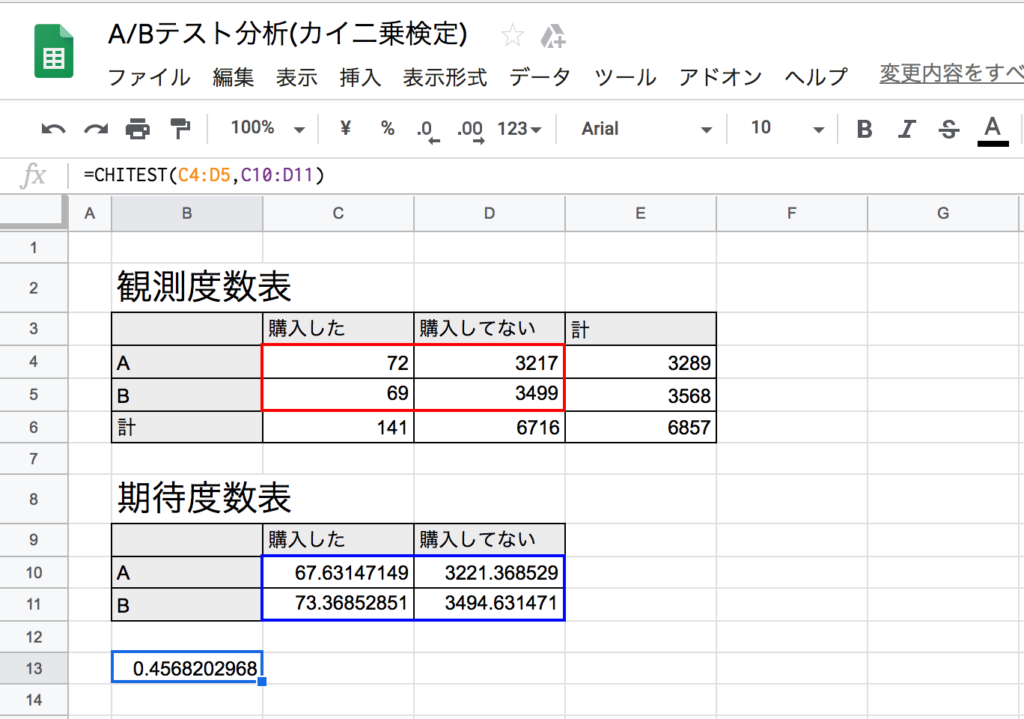



スプレッドシートでピアソンのカイ二乗検定 独立性の検定 を行う方法 たぬハック




2つ変数は独立なのか ーカイ二乗検定



Http Leo Ec T Kanazawa U Ac Jp Nakayama Edu File Prob Sta 11 Pdf



Http Cogpsy Educ Kyoto U Ac Jp Personal Kusumi Datasem11 Kumaki Pdf
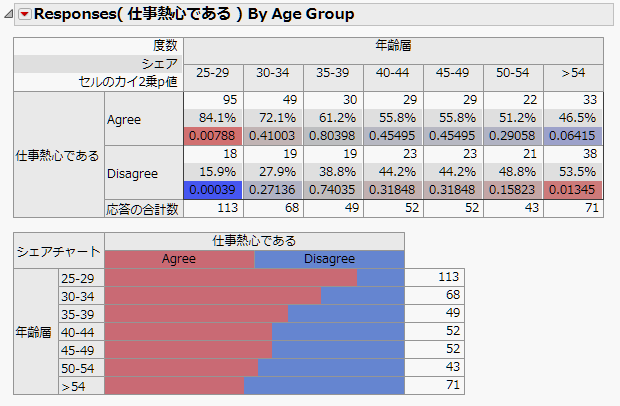



セルのカイ2乗検定の例



1
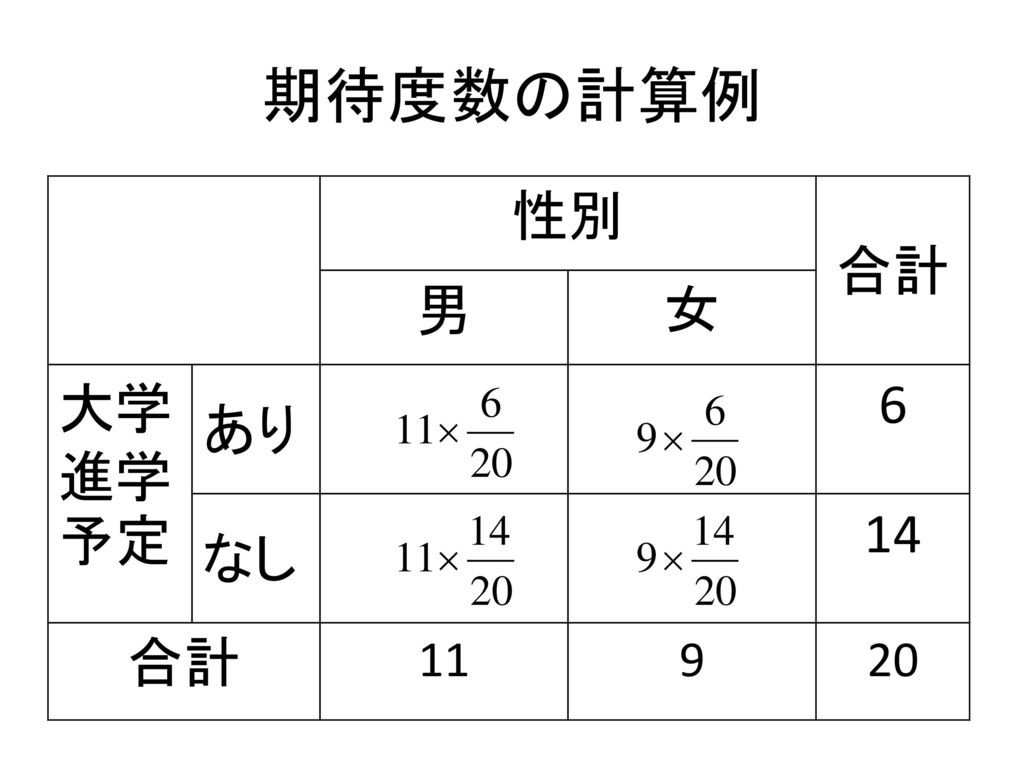



寺尾 敦 青山学院大学社会情報学部 社会統計 第4回 分割表の分析 第4章 寺尾 敦 青山学院大学社会情報学部 Ppt Download




Excel エクセルで期待値 期待度数 を計算する方法 サイコロやくじの期待値
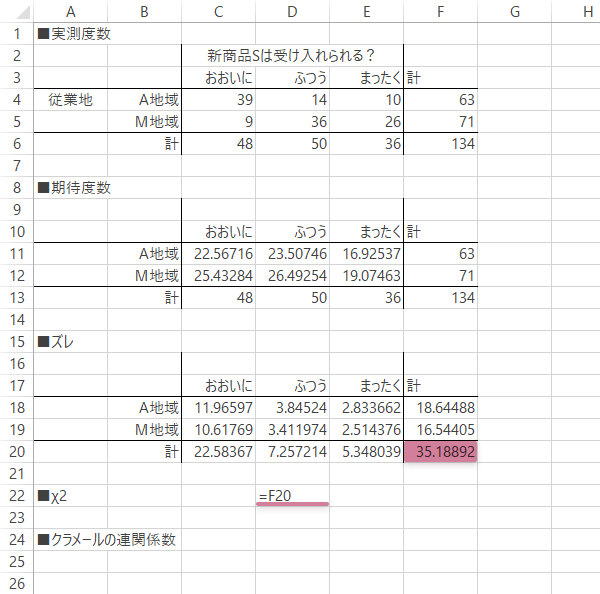



クラメールの連関係数の計算 With Excel



統計で転ばぬ先の杖 第5回 カイ二乗検定と相関係数の検定 無相関検定 にまつわるdon Ts 島田めぐみ 野口裕之 未草




カテゴリデータの関係性を検定 Excelでできるカイ二乗検定 2年でデータサイエンティストになった人が教える 初心者のためのイメージで分かるai データ分析
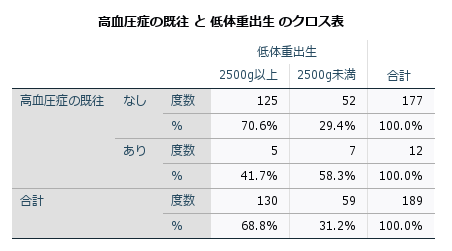



Pearsonのカイ2乗検定 Pearson S Chi Square Test Statsguild Inc スタッツギルド株式会社



1
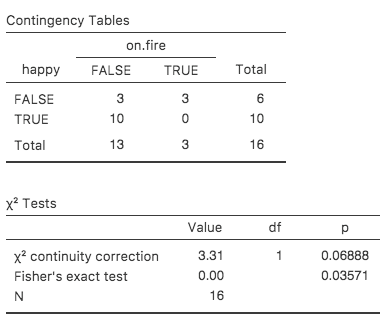



第10章 カテゴリーデータの分析 Jamoviで学ぶ心理統計




Spssでカイ二乗検定 フィッシャーの正確確率検定との違いやp値の解釈も いちばんやさしい 医療統計




分布の適合度検定を行う カイ二乗検定 Python Biotech ラボ ノート



25 6 独立性の検定 エクセル統計 統計学の時間 統計web
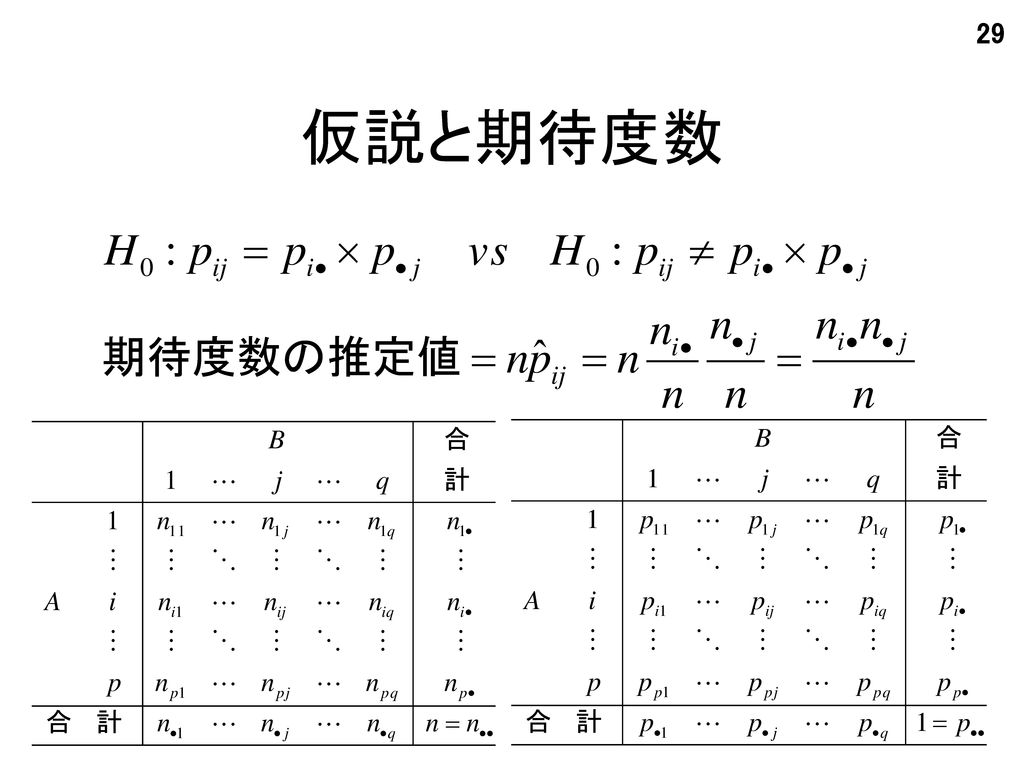



分割表データの分析 With The Help Of Mr Machida Ppt Download




Python とにかくわかりやすく ハンバーガー統計をやってみる Qiita




Excel16による独立性のカイ二乗検定 Youtube



Http Mizumot Com Handbook Wp Content Uploads bcbcacfd8668f96eb8d560c3c48c6e2 Pdf



カイ X 二乗値とカイ二乗検定 優技録




X2検定1 2変量



独立性の検定 カイ二乗検定 について 例題から分かる期待度数との食い違いの測り方 アタリマエ



統計分析




カイ2乗検定を身近な例で解説する 医学ノート



中高生のための 論文 入門 統計手法の具体例 川口秀樹 Note



統計で転ばぬ先の杖 第5回 カイ二乗検定と相関係数の検定 無相関検定 にまつわるdon Ts 島田めぐみ 野口裕之 未草



期待度数の求め方について教えてください 高校生600人に次のようなアンケ Yahoo 知恵袋



Chi Squared Test In Excel




独立性の検定 統計学備忘録 R言語のメモ
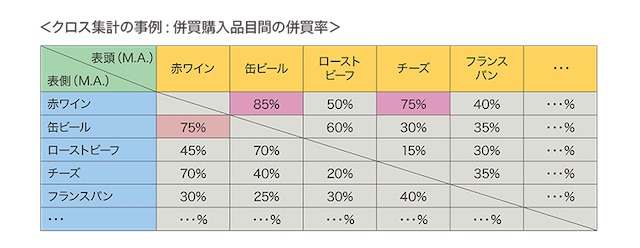



カイ二乗検定が有意だった場合におこなう残差分析をpythonで実装する キヨシの命題
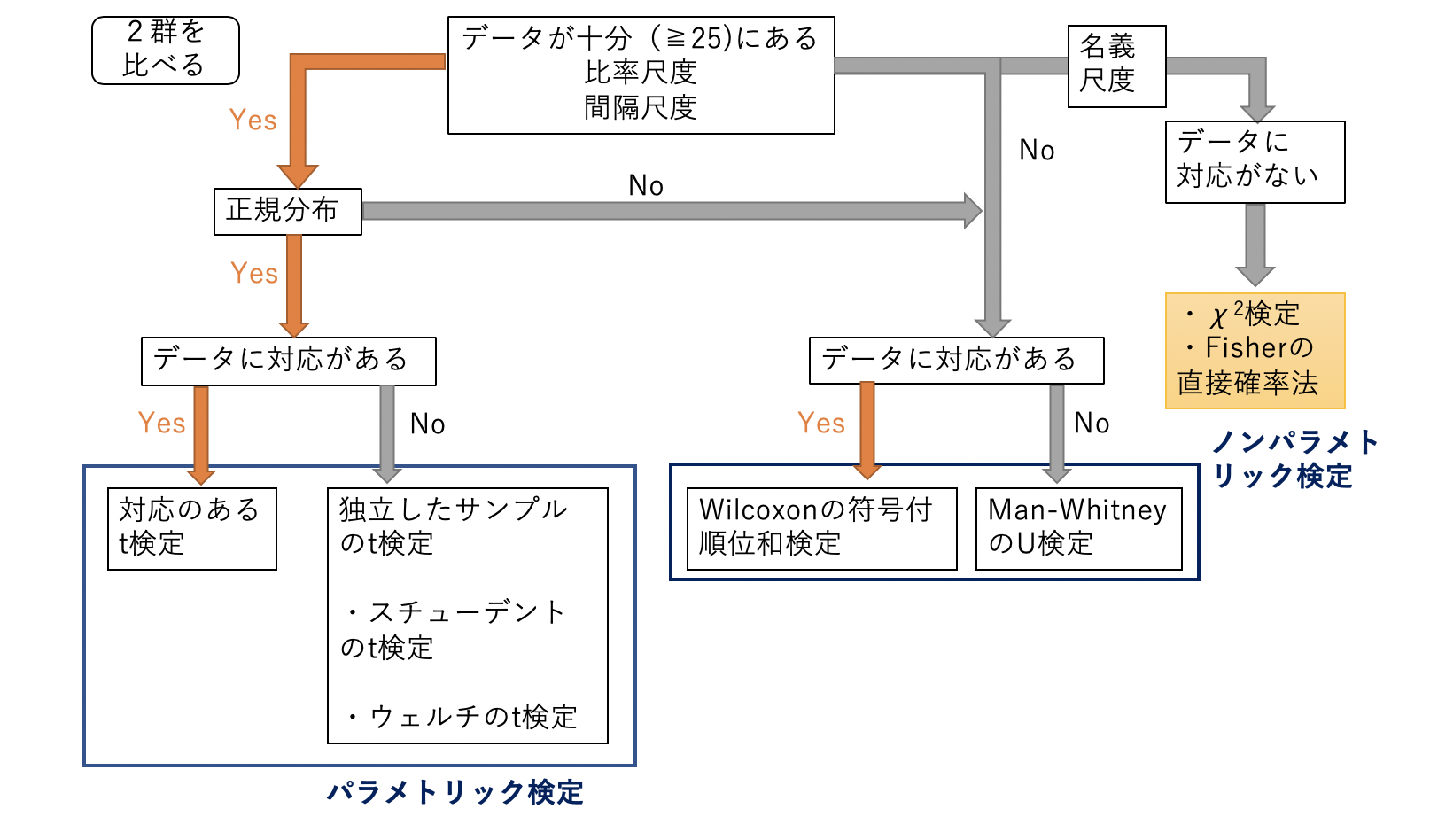



Ezrの使い方 カイ2乗 X2 検定 フィッシャーの正確検定 気楽な看護 リハビリlife
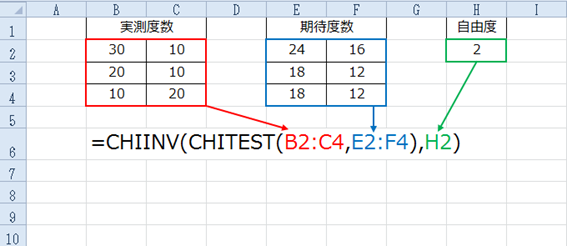



カイ2乗検定 クラメール連関係数 1 2 株式会社アイスタット 統計分析研究所
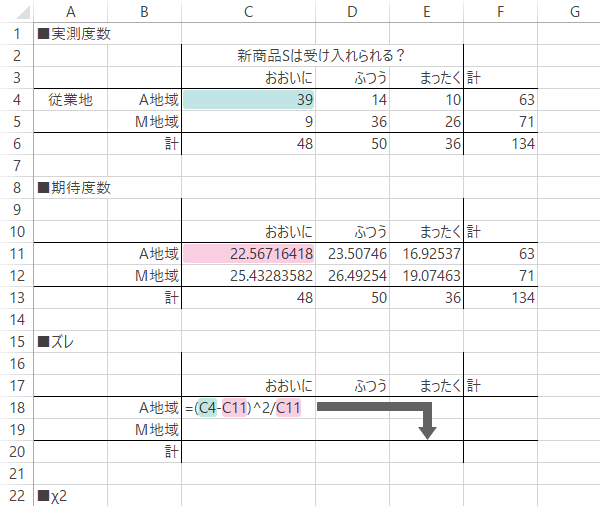



クラメールの連関係数の計算 With Excel




統計学がわかる 第3章 カイ2乗検定
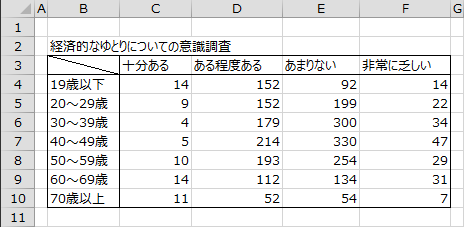



独立性の検定 エクセル統計による解析事例 ブログ 統計web




カイ二乗検定


コメント
コメントを投稿